Page 26 - 4498

case of diffusion of gases is easily to explain on the basis of MKT. But it is
necessary to distinguish such two cases: mutual-diffusion and
self-diffusion: mutual-diffusion is the phenomena of diffusion of
different gases, self-diffusion is a diffusion of molecules of the very same

gas.
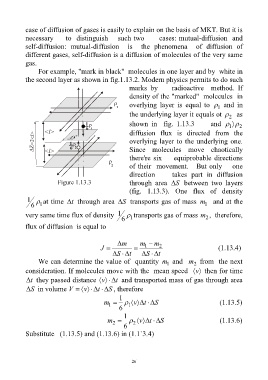
For example, "mark in black" molecules in one layer and by white in
the second layer as shown in fig.1.13.2. Modern physics permits to do such

marks by radioactive method. If
density of the "marked" molecules in
overlying layer is equal to  and in
1
the underlying layer it equals ot  as
2
shown in fig. 1.13.3 and   
1 2
diffusion flux is directed from the
overlying layer to the underlying one.

Since molecules move chaotically
there're six equiprobable directions
of their movement. But only one

direction takes part in diffusion
Figure 1.13.3 through area S between two layers
(fig. 1.13.3). One flux of density

1  at time t through area S transports gas of mass m and at the
6 1 1

very same time flux of density 1  transports gas of mass m , therefore,
6 1 2
flux of diffusion is equal to

 m m  m
J   1 2 (1.13.4)
 S  t   S  t 
We can determine the value of quantity m and m from the next
2
1
consideration. If molecules move with the mean speed v then for time
t  they passed distance v  t and transported mass of gas through area
 S in volume V   v  t  S , therefore

1
m   1  v  t  S (1.13.5)
1
6
1
m   2  v  t  S (1.13.6)
2
6
Substitute (1.13.5) and (1.13.6) in (1.1`3.4)

26