Page 28 - 4498

force of friction which acts on one square meter of two layers of the fluid
or gas apart at a distance of 1m when the difference v between their
velocities is 1m/s. The unit for viscosity is Pascal  second [Pa.s].
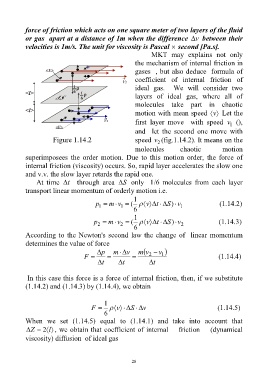
MKT may explains not only

the mechanism of internal friction in
gases , but also deduce formula of
coefficient of internal friction of

ideal gas. We will consider two
layers of ideal gas, where all of
molecules take part in chaotic

motion with mean speed v Let the
first layer move with speed v (),
1
and let the second one move with
Figure 1.14.2 speed v (fig.1.14.2). It means on the
2
molecules chaotic motion

superimposees the order motion. Due to this motion order, the force of
internal friction (viscosity) occurs. So, rapid layer accelerates the slow one

and v.v. the slow layer retards the rapid one.
At time t through area S only 1/6 molecules from each layer
transport linear momentum of orderly motion i.e.
1
p  m v  (   v  t  S ) v (1.14.2)
1
1
1
6
1
p  m v  (   v  t  S ) v 2 (1.14.3)
2
2
6
According to the Newton's second law the change of linear momentum
determines the value of force
 p m  v m v  v 
F    2 1 (1.14.4)
t  t  t 

In this case this force is a force of internal friction, then, if we substitute
(1.14.2) and (1.14.3) by (1.14.4), we obtain

1
F    v  S  v (1.14.5)
6
When we set (1.14.5) equal to (1.14.1) and take into account that
Z  2 l  , we obtain that coefficient of internal friction (dynamical

viscosity) diffusion of ideal gas

28