Page 51 - 4388

T q 
T N= . (8.3)
R
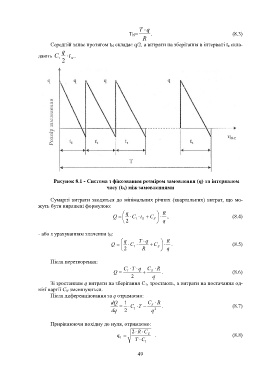
Середній запас протягом t N складає q/2, а витрати на зберігання в інтервалі t x скла-
q
дають C t  .
1 N
2

Рисунок 8.1 - Система з фіксованим розміром замовлення (q) та інтервалом
часу (t N) між замовленнями

Сумарні витрати зводяться до мінімальних річних (квартальних) витрат, що мо-
жуть бути виражені формулою:
 q  R
Q    C  t  C   , (8.4)
S
1
S
 2  q

- або з урахуванням значення t N:
 q T q   R
Q    C   C   . (8.5)
S
1
 2 R  q

Після перетворення:
C T  q  C  R
Q  1  S . (8.6)
2 q
Зі зростанням q витрати на зберігання С 1, зростають, а витрати на постачання од-
нієї партії C N зменшуються.
Після диференціювання за q отримаємо:
dQ 1 C  R
  C  T  S . (8.7)
dq 2 1 q 2

Прирівнюючи похідну до нуля, отримаємо:
2 R  C
q  S . (8.8)
0
T  C
1

49