Page 8 - 4299

4 ЗАВДАННЯ НА КОНТРОЛЬНУ РОБОТУ
з дисципліни «Алгоритми і методи обчислень»

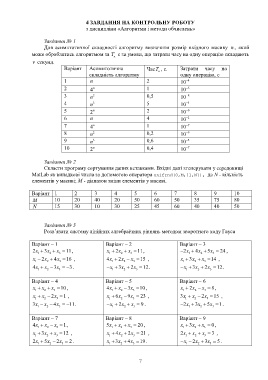
Завдання № 1
Для асимптотичної складності алгоритму визначити розмір вхідного масиву n , який
може оброблятись алгоритмом за T с за умови, що затрати часу на одну операцію складають
a
v секунд.
Варіант Асимптотична ЧасT , с. Затрати часу на
a
складність алгоритму одну операцію, с
1 n 2 10

4
n
5

2 4 1 10
3 n 0,5 10
2
8

3
4 n 5 10
3

6

n
5 2 2 10

6 n 4 10
2
n
7 4 1 10
7

8 n 0,2 10

2
9
3
5
9 n 0,6 10

7
10 2 0,4 10

n

Завдання № 2
Скласти програму сортування даних вставками. Вхідні дані згенерувати у середовищі
MatLab як випадкові числа за допомогою оператора unifrnd(0,M,[1,N]), де N - кількість
елементів у масиві; M - діапазон зміни елементів у масиві.

Варіант 1 2 3 4 5 6 7 8 9 10
M 10 20 40 20 50 60 50 35 75 80
N 15 30 10 30 25 45 60 40 40 50

Завдання № 3
Розв’язати систему лінійних алгебраїчних рівнянь методом зворотного ходу Гауса

Варіант – 1 Варіант – 2 Варіант – 3
2x  3x  x  11, x  2x  x  11,  2x  4x  5x  24 ,
1 2 3 1 2 3 1 2 3
x  2x  4x  16 , 4x  2x  x  15 , x  3x  x  14 ,
1 2 3 1 2 3 1 2 3
3
4x  x  3x   .  x  3x  2x  12.  x  3x  2x  12.
1 2 3 1 2 3 1 2 3

Варіант – 4 Варіант – 5 Варіант – 6
x  x  x  10 , 4x  x  3x  10, x  2x  x  8,
1 2 3 1 2 3 1 2 3
x  x  2x  1 , x  6x  9x  23 , 3x  x  2x  15 ,
1 2 3 1 2 3 1 2 3
3x  x  4x   11.  x  2x  x  9 .  2x  3x  5x  .
1
1 2 3 1 2 3 1 2 3

Варіант – 7 Варіант – 8 Варіант – 9
4x  x  x  1, 5x  x  x  20 , x  3x  x  0,
1 2 3 1 2 3 1 2 3
x  3x  x  12 , x  4x  2x  21 , 2x  x  x  3 ,
1 2 3 1 2 3 1 2 3
5
2
2x  5x  2x  . x  3x  4x  19.  x  2x  3x  .
1 2 3 1 2 3 1 2 3

7