Page 67 - 4234
P. 67
Figure 7.8 Figure 7.9
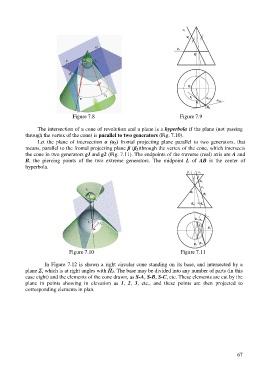
The intersection of a cone of revolution and a plane is a hyperbola if the plane (not passing
through the vertex of the cone) is parallel to two generators (Fig. 7.10).
Let the plane of intersection α (α 2) frontal projecting plane parallel to two generators, that
means, parallel to the frontal projecting plane β (β 2)through the vertex of the cone, which intersects
the cone in two generators g1 and g2 (Fig. 7.11). The endpoints of the traverse (real) axis are A and
B, the piercing points of the two extreme generators. The midpoint L of AB is the center of
hyperbola.
Figure 7.10 Figure 7.11
In Figure 7.12 is shown a right circular cone standing on its base, and intersected by a
plane Σ, which is at right angles with Π 2. The base may be divided into any number of parts (in this
case eight) and the elements of the cone drawn, as S-A, S-B, S-C, etc. These elements are cut by the
plane in points showing in elevation as 1, 2, 3, etc., and these points are then projected to
corresponding elements in plan.
67