Page 16 - 208_

Теоретичні відомості

Методи пошуку мінімума функції однієї змінної

Функція f(x) має локальний мінімум у точці x , якщо існує
0
деяка додатна величина  така, що якщо | x - x | < , то
0
f(x)≥f(x ), тобто, якщо існує окіл точки x такий, що для всіх
0
0
значень x в цьому околі f(x) більше f(x ). Функція f(x) має
0
глобальний мінімум у точці x*, якщо для всіх x справедлива
нерівність f(x)≥f(x*).

На рисунку 2.1 зображено функцію f(x), яка має локальний
мінімум в точці x і глобальний мінімум в точці x*.
0
Класичний підхід до задачі знаходження значень х і x* полягає
0
в пошуку рівнянь, які вони повинні задовільняти. Показана на

рисунку 2.1 функція та її похідні неперервні, і видно, що в
точках x та x* похідна f’(x) (градієнт функції) дорівнює нулю.
0
Отже, x та x* будуть розв’язками рівняння
0
f’(x) = 0 (2.1)

y

y=f(х)

х*
0 х с x m х 0 х

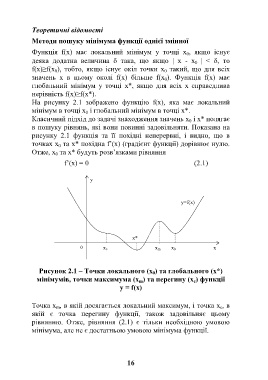
Рисунок 2.1 – Точки локального (x ) та глобального (x*)
0
мінімумів, точки максимума (x ) та перегину (x ) функції
m
с
y = f(x)

Точка x , в якій досягається локальний максимум, і точка x , в
c
m
якій є точка перегину функції, також задовільняє цьому
рівнянню. Отже, рівняння (2.1) є тільки необхідною умовою

мінімума, але не є достатньою умовою мінімума функції.

16