Page 69 - 169

Найбільш зручними для апроксимації вважають дробово-раціональні
функції, на практиці більшість функціональних залежностей простіше
апроксимувати саме такими функціями.
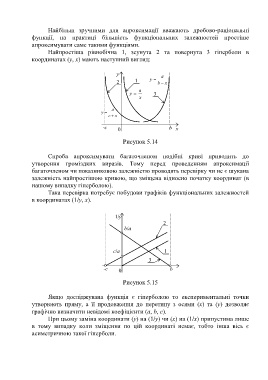
Найпростіша рівнобічна 1, зсунута 2 та повернута 3 гіперболи в
координатах (y, x) мають наступний вигляд:

y a
2 1 y  b  x
a
y  3
x

a
y 
c  x

-с 0 b x

Рисунок 5.14

Спроба апроксимувати багаточленом подібні криві приводить до
утворення громіздких виразів. Тому перед проведенням апроксимації
багаточленом чи показниковою залежністю проводять перевірку чи не є шукана
залежність найпростішою кривою, що зміщена відносно початку координат (в
нашому випадку гіперболою).
Така перевірка потребує побудови графіків функціональних залежностей
в координатах (1/y, x).

1/y
2
b/a

c/a 1
3

-с 0 b

Рисунок 5.15

Якщо досліджувана функція є гіперболою то експериментальні точки
утворюють пряму, а її продовження до перетину з осями (x) та (y) дозволяє
графічно визначити невідомі коефіцієнти (a, b, c).
При цьому заміна координати (y) на (1/y) чи (x) на (1/x) припустима лише
в тому випадку коли зміщення по цій координаті немає, тобто інша вісь є
асиметричною такої гіперболи.