Page 37 - 169

техніці, системи стандартних сигналів: Чебишева, Лежандра, Бесселя, поліноми
Лагера і ін. При практичній реалізації спектрального аналізу в системах
реального часу виникає потреба максимального спрощення алгоритмів обробки
даних та підвищення швидкодії обчислень.
Аналітичні вирази кореляційних моделей, які базуються на функції
еквівалентності, що забезпечує максимальне спрощення алгоритмів обчислень
і, відповідно, підвищує їх швидкодію, дозволяють реалізувати математичний
апарат спектрального аналізу без використання операцій множення та
піднесення до квадрату у вигляді:
n 
G ( )   z[ f , e ( )] (3.23)
k
k
x
k 1
де: e k ( ) – набір базисних функцій;
   f k , при f k  e k ,
z [ f , e ]  z  
k k e , при f  e .
 k k k
f – нормована функція автокореляції еквівалентності.
k
З розвитком цифрової обчислювальної техніки та апарату дискретної
математики для обчислення спектрів частіше використовуються системи
негармонійних ортогональних функцій Уолша, Хаара, Віленкіна-Крестенсона
та ін. Спектральна обробка в базисах Уолша та Хаара, найбільше
задовольняють вимогам високої швидкодії та спрощення алгоритмів
спектрального аналізу. При виборі базисних функцій в спектральній обробці
сигналів, крім простоти формування стандартних сигналів, намагаються
досягнути мінімальної кількості гармонік, необхідної для апроксимації сигналу.
Більшість технологічних об’єктів мають ергодичний характер зміни
станів, для яких нормована автокореляцій на функція еквівалентності f ( ) j
xx
при великих зміщеннях ( j ) прямує до нуля або приймає випадкові значення,
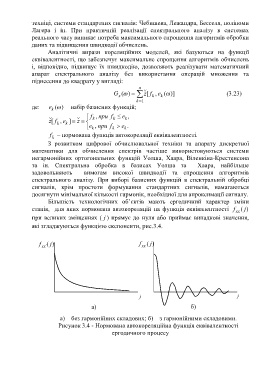
які згладжуються функцією експоненти, рис.3.4.

f xx ( ) j f xx ( ) j

j j
а) б)

а) – без гармонійних складових; б) – з гармонійними складовими.
Рисунок 3.4 - Нормована автокореляційна функція еквівалентності
ергодичного процесу