Page 38 - 169

Для сигналів (tx ) з широким спектром найкращу збіжність забезпечує
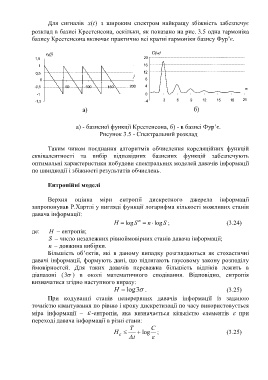
розклад в базисі Крестенсона, оскільки, як показано на рис. 3.5 одна гармоніка
базису Крестенсона включає практично всі кратні гармоніки базису Фур’є.

e k (j) G(w)
1,5 20
1 16
0,5 12
j
0 8
-0,5 50 100 150 200 4
w
-1 0
-1,5 -4 3 6 9 12 15 18 21
а) б)

а) - базисної функції Крестенсона, б) - в базисі Фур’є.
Рисунок 3.5 - Спектральний розклад

Таким чином поєднання алгоритмів обчислення кореляційних функцій
еквівалентності та вибір відповідних базисних функцій забезпечують
оптимальні характеристики побудови спектральних моделей давачів інформації

по швидкодії і збіжності результатів обчислень.

Ентропійні моделі

Верхня оцінка міри ентропії дискретного джерела інформації
запропонував Р.Хартлі у вигляді функції логарифма кількості можливих станів
давача інформації:
n
H  log S  n log S ; (3.24)
де: H – ентропія;
S – число незалежних рівноймовірних станів давача інформації;
n – довжина вибірки.
Більшість об’єктів, які в даному випадку розглядаються як стохастичні
давачі інформації, формують дані, що підлягають гаусовому закону розподілу

ймовірностей. Для таких давачів переважна більшість відліків лежить в
діапазоні ( 3 ) в околі математичного сподівання. Відповідно, ентропія
визначатися згідно наступного виразу:
H  log 3  . (3.25)

При кодуванні станів неперервних давачів інформації із заданою
точністю квантування по рівню і кроку дискретизації по часу використовується
міра інформації –  -ентропія, яка визначається кількістю елементів  при
переході давача інформації в різні стани:
T C
H   log ; (3.25)

t 