Page 156 - 157

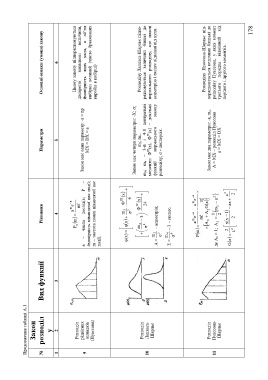
Продовження таблиці А.1
Закон

№ розподіл Вид функції Рівняння Параметри Основні ознаки (умови) закону
у
1 2 3 4 5 6

e
a m  a
P  m  Цьому закону підпорядковуються
Розподіл a m !
рідкісних Закон має один параметр: -a = np дискретні випадкові величини,
9 a – число дослідів; Р – ймовірність яких мала, а об’єм
випадків ймовірність цікавлячої нас події; МХ = DX = а
(Пуассона) m – частота появи цікавлячої нас вибірки великий (число бракованих
виробів в вибірці)
події.

 m 3 Ф III   
x
 )x(     x 3   
   6  
Закон має чотири параметри: -Х; ;
x
  m 4  Ф IV    m 3; m 4. Розподілу Лапласа-Шарльє підпо-

Розподіл   4    3  
10 Лапласа-      24   m 3; m 4 – 3-й і 4-й центральні рядковуються величини близкі до
ІІІ
IV
моменти; Ф (х), Ф (х) – довільні нормального розподілу, але маючі
Шарльє m 3
A  3 - асиметрія; функції нормального закону асиметрію і ексцес відмінні від нуля.
 розподілу;  - дисперсія.
m 4
E  4  3 - ексцес.

a m e a a m e a
P  m  
m ! m !
Розподілу Пуассона-Шарльє під-
 A  A 2 G  x
0
Розподіл Закон має два параметри: -a, m 2. порядковуються величини близькі до
11 Пуассона- де А 0 = 1; A  1 m  a 2  А = МХ – розподіл Пуассона розподілу Пуассона, у яких момент
Шарльє 2 2 2 а = МХ = DХ третього порядка відмінний від
2  x  1x  a 2  першого і другого моментів.
G   x 2   ax  
   2 2  

178