Page 155 - 157

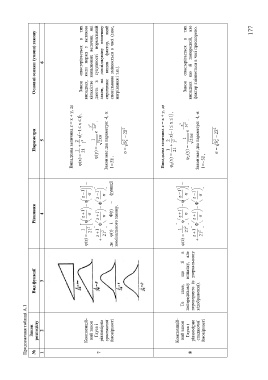
Продовження таблиці А.1
Закон
№ Вид функції Рівняння Параметри Основні ознаки (умови) закону
розподілу
1 2 3 4 5 6

Випадкова величина z = x + y, де
1 2
) x (    x  l  x   l , Закон спостерігається в тих
1    lz   z   l l 2 l 2
Композицій-  )z(  2           випадках, коли поряд з великою
ний закон l 2         1  x 2 2 кількістю випадкових величин, які
Гауса і z  l    lz  z   l ) y (   e 2 . дають в сукупності нормальний
7  Ф     Ф   2
рівномірно 2        закон, на досліджувану величину
зростаючої l 2    Закон має два параметри: -l, . спричиняє вплив фактор, який
ймовірності де (t) і Ф(t) – функції z 3 l  , сповільнено змінюється в часі (знос,
номінального закону. нагрівання і т.п.).
2 2
  S  z 2
z

Випадкова величина z = x + y, де
1 2
 1 ) x (   2 x  l  x   l ,
l 2 l
Композицій- 1    lz   z   l
ний закон Те саме, що й в  )z(  2           1  x 2 2 Закон спостерігається в тих
Гауса і попередньому випадку, але l 2          2 ) y (  e 2 .
8 2 випадках що й попередній, але
рівномірно перевернуто (в дзеркальному z  l    lz   z   l фактор змінюється в часі прискорено.
Ф


спадаючої відображенні).  2       Ф     Закон має два параметри: -l, .
ймовірності l 2    - l  z 3 ,

2
  S  z 2 2
z

177