Page 152 - 157

Додаток A
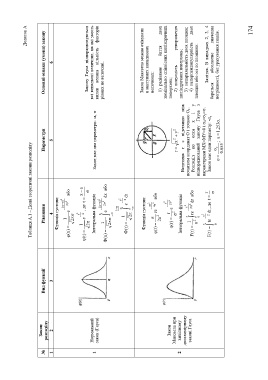
Таблиця А.1 – Деякі теоретичні закони розподілу

Закон
№ Вид функції Рівняння Параметри Основні ознаки (умови) закону
розподілу
1 2 3 4 5 6
Функція густини
x (  ) a 2
1  2
) x (   e 2 або
2 
2
t
1  x  a
 ) t (  e 2 , де t
2  Закону Гауса підпорядковуються
Нормальний всі випадкові величини, на які мають
1 Інтегральна функція Закон має два параметри: -а, 
закон (Гауса) вплив велика кількість факторів
x x (  )a 2
1  2 рівних по величині.
Ф ) x (   e 2  dx або
2  
 
t a
 t 2
1 
Ф ) t (   e 2 dt
2 
 
Закон Максвела можна очікувати
Функція густини
в наступних випадкових
r  2
  2 величинах:
 ) r (  re a 4 або
a 2 2 1) радіальне биття двох
r 2 номінально співвісних циліндричних
Закон r  2 2
 ) r (  e поверхонь;
Максвела при  2 r  x  y 2) конусність утворюючих
2
2
2 вихідному Інтегральна функція циліндричних поверхонь;
двохвимірному r r 2 Величина r є відстанню між 3) непаралельність двох площин;
законі Гауса 1  2  2 початком координат О і точкою О 1.
) r ( F  2  re dr або Розподіл по осям х і у 4) неперпендикулярність двох
 площин або осі до площини.
0 підпорядкований закону Гауса з

t t 2 параметрами МХ=МУ=0 і  х= у=.
 r Замітка. В випадках 2, 3, 4

) t ( F  te 2 dt , де t Закон має один параметр: - r береться абсолютне значення
0   r
  ; a  . 1 253 . погрішності, без урахування знаків.
. 0 655

174