Page 15 - Семенцов Г

СВ – середнє від’ємне;
ВВ - велике від'ємне (рис2.1).
Сукупність функцій нечіткої множини aіj, і bj може бути
визначена різними шляхами, наприклад, за допомогою Z-
функцій, S-функцій, трапецевидних, експоненціальних функцій
та ін. Використання конкретної сукупності функцій залежить від
практичної ситуації.
Якщо сукупність нечіткої множини aіj, позначити як
Ubj(х), то використовуючи нечітке правило (2.2), вихід нечіткого
регулятора повинен розраховуватись
Uj = Ubj (x) · уj, (2.3)
де Uj - задовільняє (2.4)
Ubj (yk) = l (2.4)
і
U bj (x) min (U U ij (x) ) для i 1 ,...,n . (2.5)

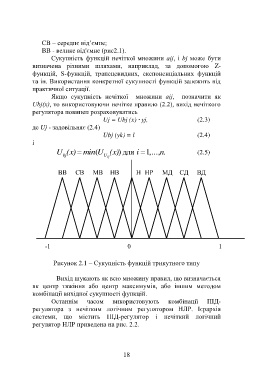
ВВ СВ МВ НВ Н НР МД СД ВД

-1 0 1

Рисунок 2.1 – Сукупність функцій трикутного типу

Вихід шукають як всю множину правил, що визначається
як центр тяжіння або центр максимумів, або іншим методом
комбінації вихідної сукупності функцій.
Останнім часом використовують комбінації ПІД-
регулятора з нечітким логічним регулятором НЛР. Ієрархія
системи, що містить ПІД-регулятор і нечіткий логічний
регулятор НЛР приведена на рис. 2.2.

18