Page 61 - 70

чітко відповідають одиниці останнього розряду, а в аналогових
приладах — деякій долі поділки.

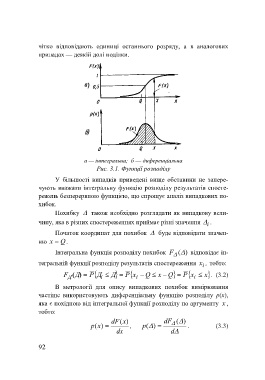
а — інтегральна; б — диференціальна
Рис. 3.1. Функції розподілу
У більшості випадків приведені вище обставини не запере-
чують вважати інтегральну функцію розподілу результатів спосте-
режень безперервною функцією, що спрощує аналіз випадкових по-
хибок.
Похибку  також необхідно розглядати як випадкову вели-
чину, яка в різних спостереженнях приймає різні значення  .
i
Початок координат для похибок  буде відповідати значен-
ню x  Q .
Інтегральна функція розподілу похибок F  ( ) відповідає ін-

тегральній функції розподілу результатів спостереження x , тобто:
i
F ( Д ) P Д   Д  P x  Q  x  Q  P x   x . (3.2)
Д i i i
В метрології для опису випадкових похибок вимірювання
частіше використовують диференціальну функцію розподілу р(х),
яка є похідною від інтегральної функції розподілу по аргументу x ,
тобто:
dF( x) dF ( )
p( x)  , p( )   . (3.3)
dx d 

92