Page 301 - 70

Якщо k 1 z  k 2 z , то вихідна величина пристрою віднімання 3 буде та-
кою:
y  y  y  Sx (8.42)
2
1
3
і не буде мати адитивної похибки.
У реальних умовах y 2 трохи відрізняється від y і в схемі (рис. 8.9 а)
1
виникає залишкова похибка  y , математичне сподівання якої буде таким:

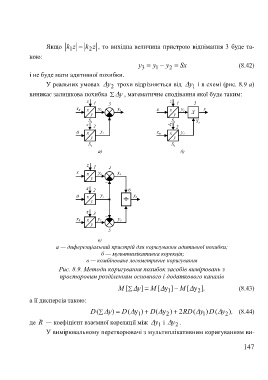
а — диференціальний пристрій для коригування адитивної похибки;
б — мультиплікативна корекція;
в — комбіноване логометричне коригування
Рис. 8.9. Методи коригування похибок засобів вимірювань з
просторовим розділенням основного і додаткового каналів

M [  y]  M [ y 1 ]  M [ y 2 , ] (8.43)

а її дисперсія такою:
D(  y)  D( y 1 )  D y( 2 ) 2 RD( y ) D( y 2 , ) (8.44)

1
де R — коефіцієнт взаємної кореляції між y і y 2 .
1
У вимірювальному перетворювачі з мультиплікативним коригуванням ви-
147