Page 10 - 6736

disp('Вивести результати обчислень?')
disp('Якщо так - введіть "1"; інакше - "0"');
k=input('k=');
if k==1
disp('Амплітуда:a= ')
disp(c);
disp('Частота:omega= ')
disp(omega);
end
%-----------------------------------------------------------------------
%Побудова графіка автоколивань
figure
t=0:0.1:50;
Z=c*sin(omega*t);
plot(t,Z)

Рівняння (2) необхідно записати у m-файл fun_Solve,який для даної задачі має такий
вигляд:

function fx=fun_Solve(x,b,s)
%=================================
%Функія f(x) у задачі f(x)=0
%=================================
fx=asin(b/x)+(b/x)*sqrt(1-(b/x)^2)-s;

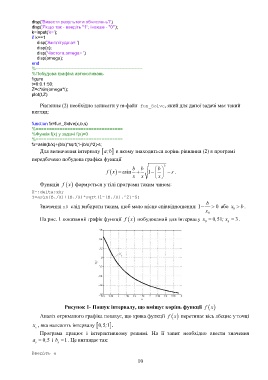
Для визначення інтервалу a;b в якому знаходиться корінь рівняння (2) в програмі
передбачено побудова графіка функції
2
b b  b 
f   asinx   1    s .
x x  x 
Функція   x формується у тілі програми таким чином:
f
X=:delta:xk;
Y=asin(B./X)+(B./X)*sqrt(1-(B./X).^2)-S;
b
Значення x0 слід вибирати таким, щоб мало місце співвідношення: 1  0 або x  .
b
0
x
0
f
3
На рис. 1 показаний графік функції   x побудований для інтервалу x  0 51, ; x  .
0 k

Рисунок 1- Пошук інтервалу, що вміщує корінь функції   x
f
f
Аналіз отриманого графіка показує, що крива функції   x перетинає вісь абсцис у точці

x , яка належить інтервалу 0 5 1, ; .
s
Програма працює і інтерактивному режимі. На її запит необхідно ввести значення
1
a  0 5, і b  . Це виглядає так:
s s

Введіть а
10