Page 22 - 6416


 b   1  1

третій стовпець таблиці буде провідним. Із умови min :  i   min : 7 ; 36  7


il a  0   a 0 il   il a  0  13  13
0
0
випливає, що провідним буде рядок, який асоційований зі змінноюr . На перетині провідного
1
рядка і провідного стовпця розміщений провідний елемент. Після того як знайдений
провідний елемент перераховуємо всі елементи таблиці.
К5. Оскільки в індексному рядку немає додатних елементів, то отримали оптимальний

розв’язок задачі. Так як   0R r  , то отримали оптимальний розв’язок x  1 10 і x  3 8 ,
1 2
13 13
*
який є і допустимим. Оптимальне значення цільової функції   обчислюється
R x
 11 
підстановкою отриманого розв’язку у вираз для цільової функції і дорівнює  141  .

 13 
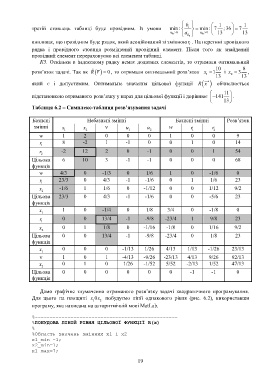
Таблиця 6.2 – Симплекс-таблиця розв’язування задачі

Базисні Небазисні змінні Базисні змінні Розв’язок
змінні x x  u u w r r
1 2 1 2 1 2
w 1 2 0 0 0 1 0 0 9
r 8 -2 1 -1 0 0 1 0 14
1
r -2 12 2 0 -1 0 0 1 54
2
Цільова 6 10 3 -1 -1 0 0 0 68
функція
w 4/3 0 -1/3 0 1/6 1 0 -1/6 0
r 23/3 0 4/3 -1 -1/6 0 1 1/6 23
1
x -1/6 1 1/6 0 -1/12 0 0 1/12 9/2
2
Цільова 23/3 0 4/3 -1 -1/6 0 0 -5/6 23
функція
x 1 0 -1/4 0 1/8 3/4 0 -1/8 0
1
r 0 0 13/4 -1 -9/8 -23/4 1 9/8 23
1
x 0 1 1/8 0 -1/16 -1/8 0 1/16 9/2
2
Цільова 0 0 13/4 -1 -9/8 -23/4 0 1/8 23
функція
x 0 0 0 -1/13 1/26 4/13 1/13 -1/26 23/13
1
 1 0 1 -4/13 -9/26 -23/13 4/13 9/26 92/13
x 0 1 0 1/26 -1/52 5/52 -2/13 1/52 47/13
2
Цільова 0 0 0 0 0 0 -1 -1 0
функція

Дамо графічне тлумачення отриманого розв’язку задачі квадратичного програмування.
Для цього на площині x 0x побудуємо лінії однакового рівня (рис. 6.2), використавши
1 2
програму, яка написана на алгоритмічній мові MatLab.

%================================================
%ПОБУДОВА ЛІНІЙ РІВНЯ ЦІЛЬОВОЇ ФУНКЦІЇ R(x)
%================================================
%Область значень змінних x1 i x2
x1_min=-1;
x2_min=1;
x1_max=7;
19