Page 23 - 6416

x2_max=9;
h=0.05;
[x1,x2]=meshgrid(x1_min:h:x1_max,x2_min:h:x2_max);
%------------------------------------------------
%Коефіцієнти цільової функції
f1=-14;
f2=-54;
a1=4;a2=-2;a3=6;
R=f1*x1+f2*x2+a1*x1.^2+a2*x1.*x2+a3*x2.^2;
%------------------------------------------------
%Побудова ліній рівня цільової функції R(x)
L_min=-150;
L_max=-100;
hL=10;
L_opt=-141.85;
levels=L_min:hL:L_max;
contour(x1,x2,R,levels);
levels=L_opt;
hold on
contour(x1,x2,R,levels);
%------------------------------------------------
%Побудова лінії обмеження
a=4.5;b=-0.5;
x=0:10;
y=a+b*x;
hold on
plot(x,y)

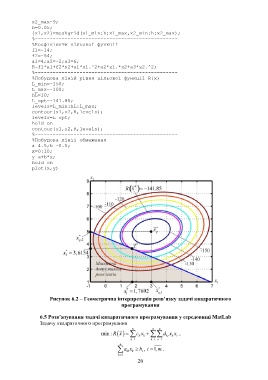
Рисунок 6.2 – Геометрична інтерпретація розв’язку задачі квадратичного
програмування

6.5 Розв’язування задачі квадратичного програмування у середовищі MatLab
Задачу квадратичного програмування
n n n
k 
min : R   x   c x  d x x ,
k
kr k
r
k 1  k 1 r 1
n
 a x  b , i  1,m .
k
ik
i
k 1
20