Page 52 - 6197

 коефіцієнти при певних змінних, що фігурують в
обмеженнях прямої задачі, стають коефіцієнтами лівої
частини відповідного обмеження двоїстої задачі, а
коефіцієнти, що фігурують при тих же змінних у виразі для
цільової функції прямої задачі, стають правою частиною цих
же обмежень двоїстої задачі (у табл. 1.9 затемнений
стовпець відповідає змінній x );
j
 праві частини обмежень прямої задачі стають
коефіцієнтами цільової двоїстої задачі.
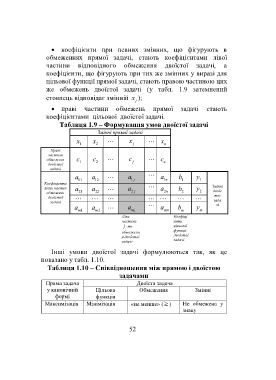
Таблиця 1.9 – Формування умов двоїстої задачі
Змінні прямої задачі
x x  x  x
1 2 j n
Праві
частини
обмежень c c  c  c
j
n
2
1
двоїстої
задачі

a a  a a b y
11 12 1 j 1n 1 1
Коефіцієнти
лівих частин a a  a  a b y Змінні
обмежень 21 22 2 j 2n 2 2 двоїс
двоїстої        тої
задачі зада
чі
a a  a  a b y
m 1 m 2 mj mn m m
Ліва Коефіці
частина єнти
j -те цільової
функції
обмеженн
я двоїстої двоїстої
задачі задачі

Інші умови двоїстої задачі формулюються так, як це
показано у табл. 1.10.
Таблиця 1.10 – Співвідношення між прямою і двоїстою
задачами
Пряма задача Двоїста задача
у канонічній Цільова Обмеження Змінні
формі функція
Максимізація Мінімізація «не менше» ( ) Не обмежена у
знаку
52