Page 109 - 6099

r sin θδφ
rδθ

δr

θ + δθ
θ

r r + δr

φ φ + δφ

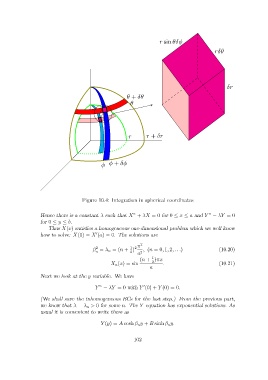
Figure 10.4: Integration in spherical coordinates

Hence there is a constant λ such that X” + λX = 0 for 0 ≤ x ≤ a and Y ” − λY = 0
for 0 ≤ y ≤ b.
Thus X(x) satisfies a homogeneous one-dimensional problem which we well know
0
how to solve: X(0) = X (a) = 0. The solutions are

π 2
1 2
2
β = λ n = (n + ) , (n = 0, 1, 2, . . .) (10.20)
n 2 2
a
1
(n + )πx
X n (x) = sin 2 . (10.21)
a
Next we look at the y variable. We have
0
Y ” − λY = 0 with Y (0) + Y (0) = 0.
(We shall save the inhomogeneous BCs for the last step.) From the previous part,
we know that λ = λ n > 0 for some n. The Y equation has exponential solutions. As
usual it is convenient to write them as

Y (y) = A cosh β n y + B sinh β n y.

102