Page 29 - 4811
P. 29
Properties of Laplace Transform
.
Evaluating this last integral, we find
sT
1−e − 2 1
L[f(t)] = s = , s > 0.
1 − e −sT s(1 + e − sT
2 )
.
. . . .
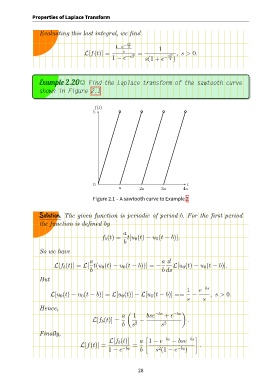
Example 2.20, Find the Laplace transform of the sawtooth curve
shown in Figure 2.1
. . . . .
f(t)
b
0 t
a 2a 3a 4a
Figure 2.1 – A sawtooth curve to Example 2
.
Solution. The given function is periodic of period b. For the first period
the function is defined by
a
f (t) = t[u (t) − u (t − b)].
0
b
0
b
So we have
a a d
L[f (t)] = L[ t(u (t) − u (t − b))] = − L[u (t) − u (t − b)].
0
0
0
b
0
b b ds
But
1 e −bs
L[u (t) − u (t − b)] = L[u (t)] − L[u (t − b)] == − , s > 0.
0
0
0
0
s s
Hence,
( )
a 1 bse −bs + e −bs
L[f (t)] = − .
b
b s 2 s 2
Finally,
[ ]
L[f (t)] a 1 − e −bs − bse −bs
b
L[f(t)] = = .
2
1 − e −bs b s (1 − e −bs )
. . . .
28