Page 105 - 4773

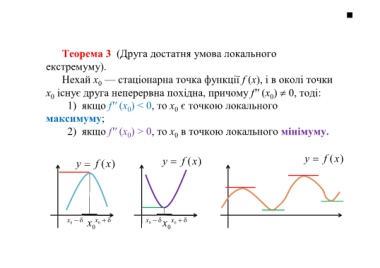
Теорема 3 (Друга достатня умова локального

екстремуму).

Нехай х — стаціонарна точка функції f (х), і в околі точки
0

х існує друга неперервна похідна, причому f′′ (х )  0, тоді:
0 0
1) якщо f′′ (х ) < 0, то х є точкою локального
0 0
максимуму;

2) якщо f′′ (х ) > 0, то х в точкою локального мінімуму.
0 0

y  f (x ) y  f (x ) y  f (x )

x   x   x   x  
0 x 0 0 x 0
0 0