Page 44 - 4719

функція, або обмеження, або те й інше не опуклі. Задачі
неопуклого програмування називають також
багатоекстремальними.
У задачах електроенергетики маємо справу з нелінійним
опуклим програмуванням, для чого розроблені загальні
ефективні методи.
Функція f (x ) є опукла на інтервалі a ≤ x ≤ b , якщо для
будь-яких 2-х точок x та x з цього інтервалу справедлива
1
2
нерівність:
{ x +
f λ 1 1 ( − λ ) x ⋅ 2 }≤ λ f (x 1 ) + 1 ( − λ ) f ⋅ (x 2 ) , (7.2)
при 0 ≤ λ ≤ 1.
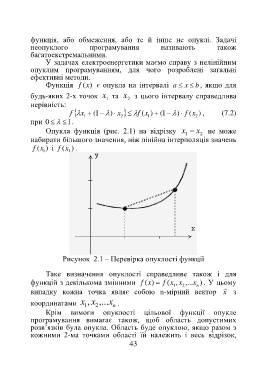
Опукла функція (рис. 2.1) на відрізку x − x не може
1
2
набирати більшого значення, ніж лінійна інтерполяція значень
f (x 1 ) і (x .
f
)
1

Рисунок 2.1 – Перевірка опуклості функції

Таке визначення опуклості справедливе також і для
функцій з декількома змінними (xf ) = f (x 1 , x 2 ,...x n ) . У цьому

випадку кожна точка являє собою n-мірний вектор x з
координатами x , x ,... x .
n
2
1
Крім вимоги опуклості цільової функції опукле
програмування вимагає також, щоб область допустимих
розв’язків була опукла. Область буде опуклою, якщо разом з
кожними 2-ма точками області їй належить і весь відрізок,
43