Page 151 - 4624

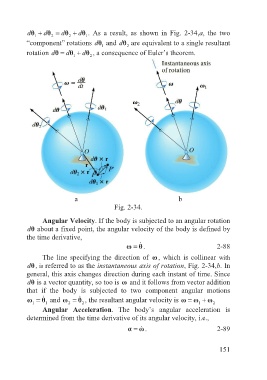
dθ 1 + dθ 2 = dθ 2 + dθ 1 . As a result, as shown in Fig. 2-34,a, the two
“component” rotations dθ and dθ are equivalent to a single resultant
1
2
rotation d =θ dθ 1 + dθ 2 , a consequence of Euler’s theorem.

a b
Fig. 2-34.
Angular Velocity. If the body is subjected to an angular rotation
dθ about a fixed point, the angular velocity of the body is defined by
the time derivative,
ɺ
= . 2-88
ωθ
The line specifying the direction of ω, which is collinear with
dθ, is referred to as the instantaneous axis of rotation, Fig. 2-34,b. In
general, this axis changes direction during each instant of time. Since
dθ is a vector quantity, so too is ω and it follows from vector addition
that if the body is subjected to two component angular motions
ω 1 = θ ɺ 1 and ω 2 = θ ɺ 2 , the resultant angular velocity is ωω 1 + ω 2
=
Angular Acceleration. The body’s angular acceleration is
determined from the time derivative of its angular velocity, i.e.,
α = ω ɺ . 2-89

151