Page 106 - 4588

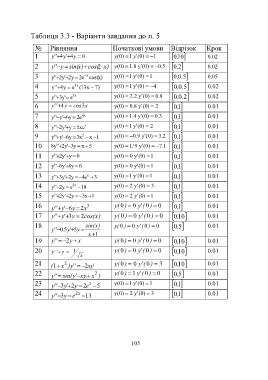
Таблиця 3.3 - Варіанти завдання до п. 5

№ Рівняння Початкові умови Відрізок Крок
1 ' ' y  4 ' y  4 y  0 ) 0 ( y  1 ) 0 ( ' y   1  100,  . 0 02
2 ' ' y  y  sin( ) x  cos(2 ) x  y ) 0 (  8 . 1 ) 0 ( ' y   5 . 0  20, . 0 02
3 ' ' y ' y 2  2  y  e 2  x cos( ) x ) 0 ( y  1 ) 0 ( ' y  1  00 .,  5 . 0 05
4 ' ' y  4 y  e 3 x ( 13 x  ) 7 ) 0 ( y  1 ) 0 ( ' y   4  00 .,  5 0. 02
5 ' ' y  ' y 3  e ) 0 ( y  2 . 2 ) 0 ( ' y  8 . 0  00 .,  2 0. 02
x
5
6 ' ' y  4 y  cos x 3 ) 0 ( y  8 . 0 ) 0 ( ' y  2  10, 0. 01
7 ' ' y  ' y y 6  e 2 x 4 ) 0 ( y  4 . 1 ) 0 ( ' y  3 . 0  10, 0. 01
8 ' ' y  ' y 2  y  5 xe ) 0 ( y  1 ) 0 ( ' y  2  10, 0. 01
x
9 ' ' y  ' y y 6  x 3 2  x  1 ) 0 ( y   9 . 0 ) 0 ( ' y  2 . 3  10, 0. 01
10 ' ' y 8 2  ' y y 3  x  5 ) 0 ( y  9 / 1 ) 0 ( ' y   1 . 7  10, 0. 01
11 ' ' y  ' y 2  y  0 ) 0 ( y  0 ) 0 ( ' y  1  10, 0. 01
12 ' ' y  ' y 6  y 8  6 ) 0 ( y  0 ) 0 ( ' y  1  10, 0. 01
13 ' ' y  ' y 3  y 2  e 4  x  3 ) 0 ( y  1 ) 0 ( ' y  1  10, 0. 01
x 3
14 ' ' y  y 2  e  18 ) 0 ( y  2 ) 0 ( ' y  3  10, 0. 01
15 ' ' y ' y 2  2  y  x 3  1 ) 0 ( y  2 ) 0 ( ' y  1  10, 0. 01
16 ' ' y  ' y  6y  2x ( y 0 ) 0 'y ( 0 ) 0  10, 0. 01
3
17 ' ' y  ' y 3 y 2 cos( ) x ( y 0 ) 0 'y ( 0 ) 0  100,  0. 01
18 sin( ) x ( y 0 ) 0 'y ( 0 ) 0  50, 0. 01
' ' y 0  . 5 'y 5 y
x  1
19 ' ' y  2 y  x ( y 0 ) 0 'y ( 0 ) 0  100,  0. 01
20 ' ' y  y  1 ( y 0 ) 0 'y ( 0 ) 0  100,  0. 01
x
21 (1 x 2 ' ' y )  2  ' xy ( y 0 ) 0 'y ( 0 ) 3  100,  0. 01
22 ' ' y  sin( ' y  xy x 2 ) ( y 0 ) 1 ('y 0 ) 0  50, 0. 01
23  ' ' y 3 'y 2 y 2e x  5 ) 0 ( y  1 ) 0 ( ' y  1  10, 0. 01
24  ' ' y 3 ey 2x  13 ) 0 ( y  2 ) 0 ( ' y  3  10, 0. 01

105