Page 62 - 4570

61

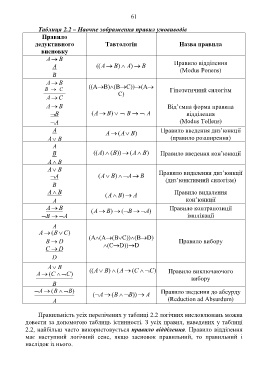
Таблиця 2.2 – Наочне зображення правил умовиводів
Правило
дедуктивного Тавтологія Назва правила
висновку
A  B
A ((A  ) B  ) A  B Правило відділення
(Modus Ponens)
B
A  B
B  C ((АВ)(ВС))(А Гіпотетичний силогізм
С)
A  C

A  B Від’ємна форма правила
 B (A  ) B   B   A відділення
 A (Modus Tollens)
A Правило введення диз’юнкції
A (A B )
A B (правило розширення)
A
B (( ) ( ))A  B  (A B ) Правило введення кон’юнкції
A B
A B Правило видалення диз’юнкції
B
A
 A (A B )   
(диз’юнктивний силогізм)
B
A B Правило видалення
(A B ) 
A
A кон’юнкції
B
A Правило контрапозиції
(A  ) B  ( B   ) A
 B   імплікації
A
A
A (B C )
(А(А(ВС))(ВD)
B  D Правило вибору
C  D (CD))D

D
A B
B
A  (C   C ) ((A B ) (A  (C   C ))) Правило виключаючого
вибору
B
 A  (B   ) B Правило зведення до абсурду
( A  (B   B ))  A
A (Reduction ad Absurdum)

Правильність усіх перелічених у таблиці 2.2 логічних висловлювань можна

довести за допомогою таблиць істинності. З усіх правил, наведених у таблиці
2.2, найбільш часто використовується правило відділення. Правило відділення
має наступний логічний сенс, якщо засновок правильний, то правильний і
наслідок із нього.