Page 11 - 4560

M y M z 
y A
  z A     ;
p max p 
J
z J y 
 (1.9)
M y M z 
y B
  z B     .
c max c 
J
z J y 
If      , just add one of the conditions (1.9), corresponding


p c
to a larger absolute value of tension.
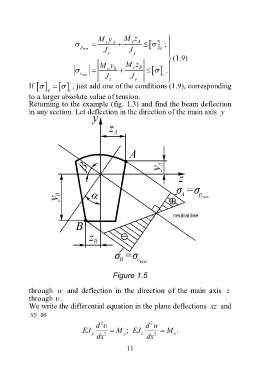
Returning to the example (fig. 1.3) and find the beam deflection
in any section. Let deflection in the direction of the main axis y

Figure 1.5

through w and deflection in the direction of the main axis z
through  .
We write the differential equation in the plane deflections xz and
xy as
2
2
d  d w
EJ  M ; EJ  M .
y 2 y z 2 z
dx dx
11