Page 40 - Microsoft Word - 4236

0
0
0
0
0
0
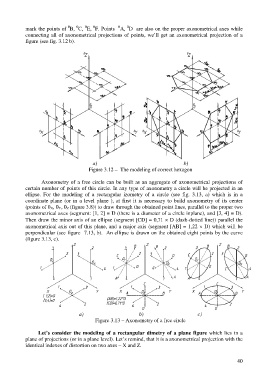
mark the points of B, C, E, F. Points A, D are also on the proper axonometrical axes while
connecting all of axonometrical projections of points, we’ll get an axonometrical projection of a
figure (see fig. 3.12 b).

а) b)
Figure 3.12 – The modeling of correct hexagon

Axonometry of a free circle can be built as an aggregate of axonometrical projections of
certain number of points of this circle. In any type of axonometry a circle will be projected in an
ellipse. For the modeling of a rectangular іzometry of a circle (see fig. 3.13, a) which is in a
coordinate plane (or in a level plane ), at first it is necessary to build axonometry of its center
(points of 0 X, 0 Y, 0 Z (figure 3.8)) to draw through the obtained point lines, parallel to the proper two
axonometrical axes (segment: [1, 2] = D (there is a diameter of a circle inplane), and [3, 4] = D).
Then draw the minor axis of an ellipse (segment [CD] = 0,71  D (dash-dotted line)) parallel the
axonometrical axis out of this plane, and a major axis (segment [AB] = 1,22  D) which will be
perpendicular (see figure 7.13, b). An ellipse is drawn on the obtained eight points by the curve
(figure 3.13, c).

а) b) c)
Figure 3.13 – Axonometry of a free circle

Let’s consider the modeling of a rectangular dimetry of a plane figure which lies in a
plane of projections (or in a plane level). Let’s remind, that it is a axonometrical projection with the
identical indexes of distortion on two axes – X and Z.

40