Page 39 - Microsoft Word - 4236

0
0
The segment ОА х (figure 3.8, a) put from a point 0 for the axes х of the axonometrical
0
system of coordinates (figure 3.8, b). Through the obtained point А х draw a straight line, parallel to
1
0 у, on which a segment is drown, equal a segment А х А. Point А is obtained from which draw a
01
.
2
02
straight line, parallel 0z . On this line draw the segment 01 А А, equal the segment of А х А. The
0
obtained point А is the isometric projection of point A. The axonometrical segments make an
axonometrical coordinate plane.
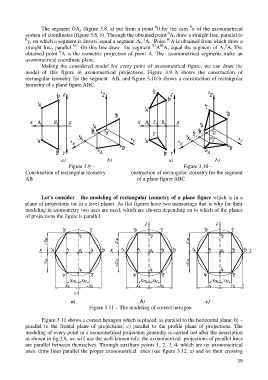
Making the considered model for every point of axonometrical figure, we can draw the
model of this figure in axonometrical projections. Figure 3.9 b shows the construction of
rectangular izometry for the segment AB, and figure 3.10 b shows a construction of rectangular
izometry of a plane figure ABC.

а) b) а) b)
Figure 3.9 – Figure 3.10 –
Construction of rectangular izometry onstruction of rectangular izometry for the segment
AB of a plane figure ABC

Let’s consider the modeling of rectangular izometry of a plane figure which is in a
plane of projections (or in a level plane). As flat figures have two measurings that is why for their
modeling in axonometry two axes are used, which are chosen depending on to which of the planes
of projections the figure is parallel.

а) b) c)
Figure 3.11 – The modeling of correct hexagon

Figure 3.11 shows a correct hexagon which is placed: a) parallel to the horizontal plane; b) –
parallel to the frontal plane of projections; c) parallel to the profile plane of projections. The
modeling of every point in a axonometrical projection generally is carried out after the description
as shown in fig.3.8, we will use the well-known rule: the axonometrical projections of parallel lines
are parallel between themselves. Through auxiliary points 1, 2, 3, 4, which are on axonometrical
axes, draw lines parallel the proper axonometrical axes (see figure 3.12, a) and on their crossing

39