Page 46 - 4202

Напруження σ α і τ α змінюються зі зміною напрямку
похилої площинки. Функції sinα і cosα періодичні, тому
при зміні кута α значення σ α і τ α спочатку
збільшуються, потім зменшуються або навпаки. Отже, є
певний кут α 0 , за якого σ α отримує максимальне чи
мінімальне значення. Щоб знайти екстремум, треба
взяти похідну від σ α (3.18) і прирівняти її до нуля:
d 

  2 x cos sin  2 y sin cos  2 cos 2  0 .
d 
.
Підставте формулу sin 2α = 2 sin 2αcos 2α , зробіть
перетворення і отримайте формулу для визначення
положення (кута нахилу) головних площинок (на яких
σ α дорівнює σ max чи σ min):

 2
tg 2   . (3.20)
0
   y
x
Разом з цим, цю ж формулу можна отримати із (3.19),
якщо дотичні напруження τ α = 0 (отримайте її). При
о
цьому площинка під кутом β 0 = α 0 + 90
(перпендикулярна до площинки α 0, як на рис 3.3) теж є
головною, тому що також задовольняє це рівняння: tg
о
2β 0 = tg (2α 0+180 ) = tg 2α 0. Отже, дві взаємно пер-
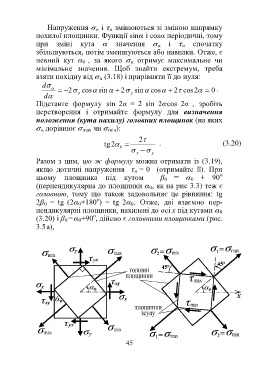
пендикулярні площинки, нахилені до осі х під кутами α 0
о
(3.20) і β 0 = α 0+90 , дійсно є головними площинками (рис.
3.5 а),

45