Page 64 - 256_

коефіцієнтів диференціального рівняння від’ємний. Відповідь
можна отримати, розглянувши хоча б одне диференціальне
рівняння І-го порядку
dy   t
T  y  t  Kx  t .
dt
Перетворимо його за Лапласом
 dy  t 
t
L  T   L y   Lt  Kx   ,
 dt 
TpY   Yp   p  KX  p ,  TppY 1  KX  p ,
Y  p K
W   p  .
X   p Tp  1
Щоб знайти перехідні характеристики, потрібно взяти
зворотне перетворення за Лапласом
p
W    K 
y    Lt 1    L 1   .
 p   p Tp 1  
Тоді    Kxty e t T   1 .
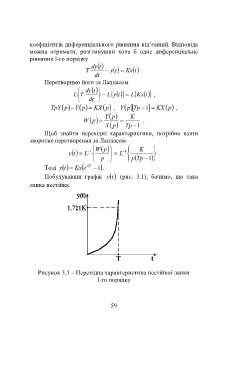
Побудувавши графік  ty (рис. 3.1), бачимо, що така
ланка нестійка.

Рисунок 3.1 – Перехідна характеристика нестійкої ланки
І-го порядку

59