Page 27 - Семенцов Г

q q 0 q 0 q 1 ,
[0,1].
Наприклад. Вірогідність (Р) безпомилкового рішення про
підйом долота для заміни, внаслідок 100%-го відпрацювання
опор і оснащення, рівна “близько 0.9”. Треба задати цю
~
інформацію у вигляді нечіткого числа P з трапецієвидною
функцією приналежності.
Розв’язок.
~
Згідно (3.2)), число P представимо у такому вигляді:
~
P 1, , 8 . 0 0.85, 0. 95 ,
де [0.8, 1] – песимістична оцінка параметра Р;
[0.85, 0.95] – оптимістична оцінка параметра Р.
~
Тоді розкладання нечіткого числа P на -рівневі множини
~
має такий вигляд: P 1 , 8 . 1 0  . 0 825 . 0 , 975 5 . 0  . 0 85 . 0 , 95 .
1
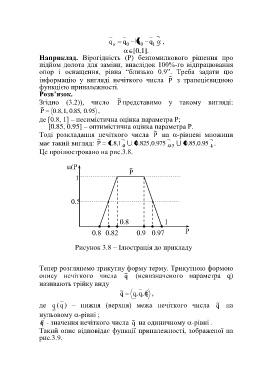
Це проілюстровано на рис.3.8.

(Р ~
) 1 P

0.5

0.8 1
0.8 0.82 5 0.9 0.97 Р
5 5 5
Рисунок 3.8 – Ілюстрація до прикладу

Тепер розглянемо трикутну форму терму. Трикутною формою
~
опису нечіткого числа q (невизначеного параметра q)
називають трійку виду
~ q € , q , q ,
q
~
де q ( q ) – нижня (верхня) межа нечіткого числа q на
нульовому -рівні ;
~
q € - значення нечіткого числа q на одиничному -рівні .
Такий опис відповідає функції приналежності, зображеної на
рис.3.9.