Page 38 - 87

37

Q, %

100

Q 4
80

Q 3
60
Q 2

40

20
Q 1

0 t, хв
10 20 100 150

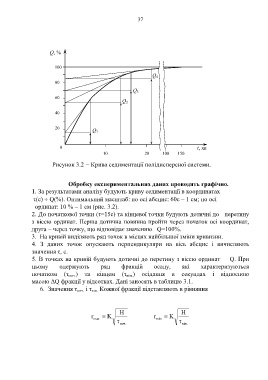
Рисунок 3.2 − Крива седиментації полідисперсної системи.

Обробку експериментальних даних проводять графічно.
1. За результатами аналізу будують криву седиментації в координатах
τ(с)  Q(%). Оптимальний масштаб: по осі абсцис: 60с – 1 см; по осі

ординат: 10 % – 1 см (рис. 3.2).
2. До початкової точки (τ=15с) та кінцевої точки будують дотичні до перетину
з віссю ординат. Перша дотична повинна пройти через початок осі координат,
друга – через точку, що відповідає значенню Q=100%.
3. На кривій виділяють ряд точок в місцях найбільшої зміни кривизни.
4. З даних точок опускають перпендикуляри на вісь абсцис і вичисляють
значення τ, с.
5. В точках на кривій будують дотичні до перетину з віссю ординат – Q. При
цьому одержують ряд фракцій осаду, які характеризуються
початком (τ поч.) та кінцем (τ кін.) осідання в секундах і відносною
масою ΔQ фракції у відсотках. Дані заносять в таблицю 3.1.
6. Значення τ поч. і τ кін. Кожної фракції підставляють в рівняння

H H
r  K r  K
max min
 
поч . кін .