Page 6 - 6449

РОЗДІЛ 1. ЛІНІЙНЕ ПРОГРАМУВАННЯ

1.1 Постановка задачі лінійного програмування. Основні
поняття теорії лінійного програмування
Розглянемо таку задачу: нехай деяка фірма займається
виготовленням n видів продукції. На виготовлення цієї продукції
витрачається сировина m видів, при чому відомими є запаси сировини
кожного виду сировини b (рис. 1.1). Крім того, відомо, що на одиницю
i
продукції кожного виду при її виготовленні витрачається певна кількість
сировини кожного типу, тобто заданими є величини a , які є елементами
ij
матриці витрат: на одиницю продукції виду A витрачається a одиниць
j
ij
сировини виду B . Ще однією інформацією, якою володіє дослідник
i
системи, є величинаGj , яка дорівнює прибутку від реалізації одиниці
продукції виду A . Необхідно встановити, скільки продукції кожного виду
j
x потрібно виготовити, щоб одержати максимальний сумарний прибуток.
j

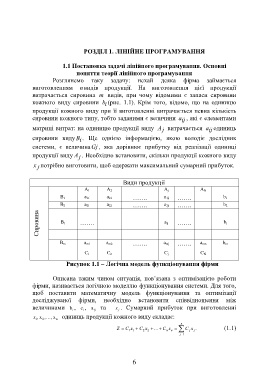
Види продукції
A 1 A 2 A j A N

a 11 a 21 a 1j
B 1 ……. ……. b 1
a 21 a 22 a 2j
B 2 ……. ……. b 2
Сировина B і ……. a ij ……. b і

B m a m1 a m2 ……. a mj ……. a mn b m
C 1 C 2 C j C N
Рисунок 1.1 – Логічна модель функціонування фірми

Описана таким чином ситуація, пов’язана з оптимізацією роботи
фірми, називається логічною моделлю функціонування системи. Для того,
щоб поставити математичну модель функціонування та оптимізації
досліджуваної фірми, необхідно встановити співвідношення між
величинами b , c , a та x . Сумарний прибуток при виготовленні
i i ij j
x , x , x , одиниць продукції кожного виду складає:
1 2 n
n
Z  C x  C x  ...  C x   C x . (1.1)
1 1 2 2 n n j j
 j 1

6