Page 16 - 6416

друга – побічною. Від добутку кутових елементів головної діагоналі віднімається добуток
кутових елементів побічної діагоналі і отримана різниця ділиться на провідний елемент.
У результаті отримуємо нову таблицю, яку суміщаємо із початковою таблицею.

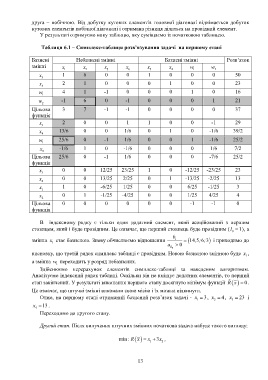
Таблиця 6.1 – Симплекс-таблиця розв’язування задачі на першому етапі

Базисні Небазисні змінні Базисні змінні Розв’язок
змінні x x x x x x w w
1 2 5 6 3 4 1 2
x 1 6 0 0 1 0 0 0 50
3
x 2 1 0 0 0 1 0 0 23
4
w 4 1 -1 0 0 0 1 0 16
1
w -1 6 0 -1 0 0 0 1 21
2
Цільова 3 7 -1 -1 0 0 0 0 37
функція

x 2 0 0 1 1 0 0 -1 29
3
x 13/6 0 0 1/6 0 1 0 -1/6 39/2
4
w 25/6 0 -1 1/6 0 0 1 -1/6 25/2
1
x -1/6 1 0 -1/6 0 0 0 1/6 7/2
2
Цільова 25/6 0 -1 1/6 0 0 0 -7/6 25/2
функція
x 0 0 12/25 23/25 1 0 -12/25 -23/25 23
3
x 0 0 13/25 2/25 0 1 -13/25 -2/25 13
4
x 1 0 -6/25 1/25 0 0 6/25 -1/25 3
1
x 0 1 -1/25 -4/25 0 0 1/25 4/25 4
2
Цільова 0 0 0 0 0 0 -1 -1 0
функція

В індексному рядку є тільки один додатний елемент, який асоційований з першим
стовпцем, який і буде провідним. Це означає, що перший стовпець буде провідним (l  1), а
0
b
змінна x стає базисною. Знову обчислюємо відношення i  14 5 6 3, ; ;  і приходимо до
1
a  0
0 il
висновку, що третій рядок симплекс таблиці є провідним. Новою базисною змінною буде x ,
1
а змінна w переходить у розряд небазисних.
1
Здійснюємо перерахунок елементів симплекс-таблиці за наведеним алгоритмом.
Аналізуємо індексний рядок таблиці. Оскільки він не вміщує додатних елементів, то перший

етап закінчений. У результаті виконання першого етапу досягнуто мінімум функції   0R x  .
Це означає, що штучні змінні виконали свою місію і їх можна відкинути.
4
3
Отже, на першому етапі отриманий базисний розв’язок задачі - x  , x  , x  23 і
1 2 3
x  13 .
4
Переходимо до другого етапу.

Другий етап. Після вилучення штучних змінних початкова задача набуде такого вигляду:

 
min : R x  x  3x ,
1
2

13