Page 6 - 4968

 b , після чого знаходяться координати точки перетину
a, f  a , b, f
 c . Будується нова січна.
січної  0;c , і знаходиться точка c, f
Вказаний процес повторюється до тих пір, поки не буде знайдено

розв’язок – точка R . Зауважимо, що ненульова координата точки
 0;c визначається за формулою:

b
c  a  f   a  a (1.3)

f   fb    a

.
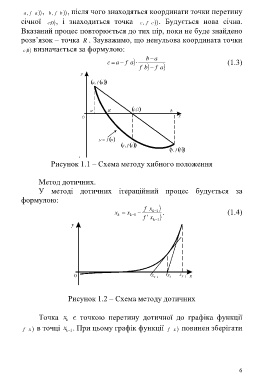
Рисунок 1.1 – Схема методу хибного положення

Метод дотичних.

У методі дотичних ітераційний процес будується за
формулою:

 f x k 1 
x  x 1  . (1.4)
k k 
f   x 1 
k

Рисунок 1.2 – Схема методу дотичних

Точка x є точкою перетину дотичної до графіка функції
k
повинен зберігати
1 
f  x в точці x . При цьому графік функції  xf
k

6