Page 61 - 4928

Основні геометричні побудови

а) б)
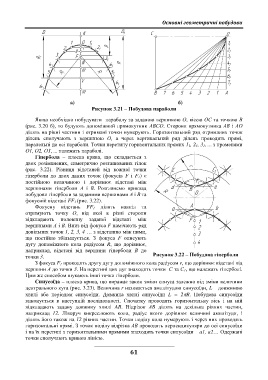
Рисунок 3.21 – Побудова параболи

Якщо необхідно побудувати параболу за заданою вершиною О, віссю ОС та точкою В
(рис. 3.20 б), то будують допоміжний прямокутник АВСО. Сторони прямокутника АВ і АО
ділять на рівні частини і отримані точки нумерують. Горизонтальний ряд отриманих точок
ділень сполучають з вершиною О, а через вертикальний ряд ділень проводять прямі,
паралельні до осі параболи. Точки перетину горизонтальних прямих 1 1, 2 1, 3 1, ... з променями
О1, О2, О3, ... належать параболі.
Гіпербола – плоска крива, що складається з
двох розімкнених, симетрично розташованих гілок
(рис. 3.22). Різниця відстаней від кожної точки
гіперболи до двох даних точок (фокусів F i F 1) є
постійною величиною і дорівнює відстані між
вершинами гіперболи А і В. Розглянемо приклад
побудови гіперболи за заданими вершинами А і В та
фокусній відстані FF 1 (рис. 3.22).
Фокусну відстань FF 1 ділять навпіл та
отримують точку О, від якої в різні сторони
відкладають половину заданої відстані між
вершинами А і В. Вниз від фокуса F намічають ряд
довільних точок 1, 2, 3, 4 … з відстанню між ними,
що постійно збільшується. З фокуса F описують
дугу допоміжного кола радіусом R, що дорівнює,
наприклад, відстані від вершини гіперболи В до
точки 3. Рисунок 3.22 – Побудова гіперболи

З фокуса F 1 проводять другу дугу допоміжного кола радіусом r, що дорівнює відстані від
вершини А до точки 3. На перетині цих дуг знаходять точки С та С 1, що належать гіперболі.
Цим же способом шукають інші точки гіперболи.
Синусоїда – плоска крива, що виражає закон зміни синуса залежно від зміни величини
центрального кута (рис. 3.23). Величина r називається амплітудою синусоїди, L – довжиною
хвилі або періодом синусоїди. Довжина хвилі синусоїди L = 2 R. Побудова синусоїди
виконується в наступній послідовності. Спочатку проводять горизонтальну вісь і на ній
відкладають задану довжину хвилі AB. Відрізок АВ ділять на декілька рівних частин,
наприклад 12. Ліворуч викреслюють коло, радіус якого дорівнює величині амплітуди, і
ділять його також на 12 рівних частин. Точки поділу кола нумерують і через них проводять
горизонтальні прямі. З точок поділу відрізка АВ проводять перпендикуляри до осі синусоїди
і на їх перетині з горизонтальними прямими знаходять точки синусоїди – а1, а2… Одержані
точки сполучають кривою лінією.

61