Page 91 - 4811

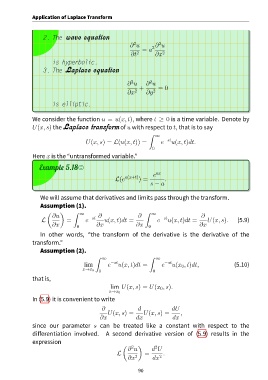
Application of Laplace Transform
.

2. The wave equation

2
2
∂ u ∂ u
= a 2
∂t 2 ∂x 2
is hyperbolic.
3. The Laplace equation

2
2
∂ u ∂ u
+ = 0
∂x 2 ∂y 2
is elliptic.
. . . . .
We consider the function u = u(x, t), where t ≥ 0 is a time variable. Denote by
U(x, s) the Laplace transform of u with respect to t, that is to say

∫
∞
U(x, s) = L(u(x, t)) = e −st u(x, t)dt.
0
.
Here x is the “untransformed variable.”

Example 5.18,
e ax
L(e a(x+t) ) = .
s − a
. . . . .
We will assume that derivatives and limits pass through the transform.
Assumption (1).

( ) ∫ ∞ ∫ ∞
∂u ∂ ∂ ∂
L = e −st u(x, t)dt = e −st u(x, t)dt = U(x, s). (5.9)
∂x 0 ∂x ∂x 0 ∂x
In other words, “the transform of the derivative is the derivative of the
transform.”

Assumption (2).
∫ ∫
∞ ∞
lim e −st u(x, t)dt = e −st u(x , t)dt, (5.10)
0
x→x 0
0 0
that is,
lim U(x, s) = U(x , s).
0
x→x 0
In (5.9) it is convenient to write

∂ d dU
U(x, s) = U(x, s) = ,
∂x dx dx
since our parameter s can be treated like a constant with respect to the

differentiation involved. A second derivative version of (5.9) results in the
expression
( 2 ) 2
∂ u d U
L = .
∂x 2 dx 2

90