Page 182 - 4737

Аналіз взаємодії представлених законів розподілу випадко-
вих величин партій та їх ритму з заданими математико-
статистичними характеристиками формують ймовірність їхнього
R
p
n
сумісного розподілу  p     при n  R та створюють
j
j
j
j
n j R j
імовірнісне поле дефіцитного стану системи, параметри якого
служать обґрунтуванням гіпотези прямолінійної двофакторної
кореляційної моделі у вигляді:
D  an  вR  c,

де D – середній рівень дефіциту;
n – величина партії деталей;

R – ритм партії деталей;
c , в , a – коефіцієнти.

Результати математико-статистичного, кореляційного аналізу
наведені нижче.
На рисунках 2.56, 2.57 графіки показують прямолінійну ко-

реляційну залежність між заданими параметрами управління
 ,D  R , n , що відповідає висунутій гіпотезі.

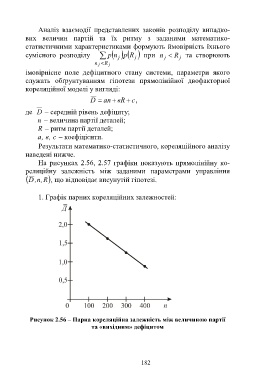
1. Графік парних кореляційних залежностей:

Рисунок 2.56 – Парна кореляційна залежність між величиною партії
та «вихідним» дефіцитом

182