Page 13 - 4707

2
Інтеграл  ydxL  від деякої функції y = f(x)
1
дорівнює площі фігури x 112x 2 під кривою f(x) (рис.1.2) і
залежить від того, яким шляхом пройти від точки 1 до
2
точки 2. Аналогічно інтеграл M  xdy теж визначається

1
шляхом від 1 до 2 і дорівнює площі фігури y 112y 2.

y

2
y 2

y 1
1

x
x 1 x 2

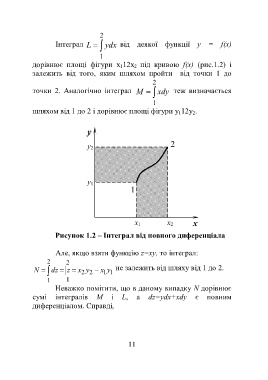
Рисунок 1.2 – Інтеграл від повного диференціала

Але, якщо взяти функцію z=xy, то інтеграл:
2 2
N   dz  z  x 2 y  x 1 y 1 не залежить від шляху від 1 до 2.
2
1 1
Неважко помітити, що в даному випадку N дорівнює
сумі інтегралів М і L, a dz=ydx+xdy є повним
диференціалом. Справді,

11