Page 28 - 4671

Крива другого порядку
До кривих другого порядку відносяться параболи, гіперболи, еліпси, кола та інші лінії,
рівняння яких не містять степенів вище другого. Прямі лінії — це окремий випадок кривих
другого порядку. Відрізняються криві другого порядку тим, що не мають точок перегину.
Загальна формула кривої другого порядку може виглядати так:
2 2 :
x +a 1у +а 2ху+а 3х+а 4у+а 5 =0
Як бачимо, п’яти параметрів цілком достатньо для опису нескінченної кривої другого
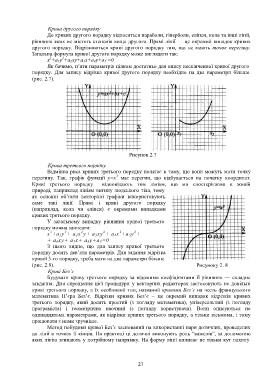
порядку. Для запису відрізка кривої другого порядку необхідно на два параметри більше
(рис. 2.7).

Рисунок 2.7

Крива третього порядку
Відмінна риса кривих третього порядку полягає в тому, що вони можуть мати точку
3
перегину. Так, графік функції y=х має перегин, що відбувається на початку координат.
Криві третього порядку відповідають тим лініям, що ми спостерігаємо в живій
природі, наприклад лініям вигину людського тіла, тому
як основні об’єкти векторної графіки використовують
саме такі лінії. Прямі і криві другого порядку
(наприклад, кола чи еліпси) є окремими випадками
кривих третього порядку.
У загальному випадку рівняння кривої третього
порядку можна записати:
3 3 2 2 2 2
х + а 1 у + a 2 х у + а 3 х y + a 4 x + а 5 у +
+ а 6 ху + а 7 х + а 8 у +a 9 =0
З нього видно, що для запису кривої третього
порядку досить дев’яти параметрів. Для задання відрізка
кривої 3-го порядку, треба мати на два параметри більше
(рис. 2.8). Рисуноку 2. 8
Криві Без’є
Будувати криву третього порядку за відомими коефіцієнтами її рівняння — складне
завдання. Для спрощення цієї процедури у векторних редакторах застосовують не довільні
криві третього порядку, а їх особливий тип, названий кривими Без’є на честь французького
математика П’єра Без’є. Відрізки кривих Без’є – це окремий випадок відрізків кривих
третього порядку, який досить простий (з погляду математика), універсальний (з погляду
програміста) і геометрично наочний (з погляду користувача). Вони описуються не
одинадцятьма параметрами, як відрізки кривих третього порядку, а тільки вісьмома, і тому
працювати з ними зручніше.
Метод побудови кривої Без’є заснований на використанні пари дотичних, проведених
до лінії в точках її кінців. На практиці ці дотичні виконують роль “важелів”, за допомогою
яких лінію згинають у потрібному напрямку. На форму лінії впливає не тільки кут нахилу

27