Page 76 - 4617

ЗГАСАЮЧІ КОЛИВАННЯ ПІД ДІЄЮ СИЛИ СУХОГО ТЕРТЯ

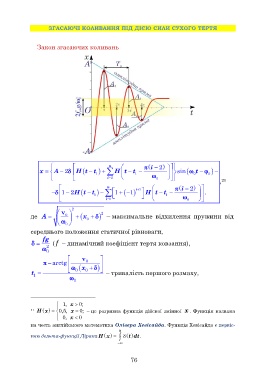
Закон згасаючих коливань

   n   i   2    
x   A  2  H tt  1   H tt  1    sin   0 t  0  



  i 3    0     ,
21
 n i   i   2  
1 


   12H tt   1  1  H tt    .


  1

  i 1    1  0   
  v 2 2
де A   0   x    – максимальне відхилення пружини від
  0  0
середнього положення статичної рівноваги,
fg
  ( f – динамічний коефіцієнт тертя ковзання),
 2
0
 v 
  arctg  x 0 

t 1    0 0 0     – тривалість першого розмаху,

 1, x  0;

   
21 Hx 0,5, x  0; – це розривна функція дійсної змінної x . Функція названа
 0, x  0

на честь англійського математика Олівера Хевісайда. Функція Хевісайда є первіс-
x
ною дельта-функції Дірака H   x     t dt .


76