Page 23 - 4604

Практичне заняття № 5. Метричні задачі

Мета – набути практичних навичок при розв’язуванні метричних задач.

Завдання:
1. Визначити дійсну величину відстані від точки D до площини, яка задана
трикутником АВС (задачу розв’язати без перетворення проекцій).
2. Дані до завдання взяти з таблиці 4.
3. Приклад виконання завдання подано на рис. 23

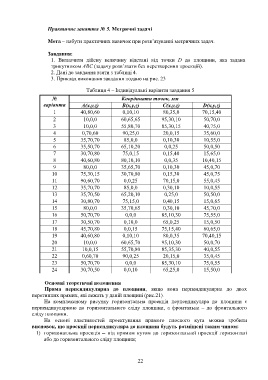
Таблиця 4 – Індивідуальні варіанти завдання 5

№ Координати точок, мм
варіанта А(x,y,z) В(x,y,z) С(x,y,z) D(x,y,z)
1 40,80,60 0,10,10 80,35,0 70,15,40
2 10,0,0 60,65,65 95,30,10 50,70,0
3 10,0,0 55,80,70 85,30,15 40,75,0
4 0,70,60 90,25,0 20,0,15 35,60,0
5 35,70,70 85,0,0 0,10,30 10,55,0
6 35,50,70 65,10,20 0,0,25 50,0,50
7 30,70,80 75,0,15 0,15,40 15,65,0
8 40,60,80 80,10,10 0,0,35 10,40,15
9 80,0,0 35,65,70 0,10,30 45,0,70
10 75,30,15 30,70,80 0,15,30 45,0,75
11 90,60,70 0,0,25 70,15,0 55,0,45
12 35,70,70 85,0,0 0,30,10 10,0,55
13 35,70,50 65,20,10 0,25,0 50,50,0
14 30,80,70 75,15,0 0,40,15 15,0,65
15 80,0,0 35,70,65 0,30,10 45,70,0
16 50,70,70 0,0,0 85,10,30 75,55,0
17 30,50,70 0,10,0 65,0,25 15,0,50
18 45,70,80 0,0,15 75,15,40 60,65,0
19 40,60,80 0,10,10 80,0,35 70,40,15
20 10,0,0 60,65,70 95,10,30 50,0,70
21 10,0,15 55,70,80 85,35,30 40,0,55
22 0,60,70 90,0,25 20,15,0 35,0,45
23 50,70,70 0,0,0 85,30,10 75,0,55
24 30,70,50 0,0,10 65,25,0 15,50,0

Основні теоретичні положення
Пряма перпендикулярна до площини, якщо вона перпендикулярна до двох
перетинних прямих, які лежать у даній площині (рис.21).
На комплексному рисунку горизонтальна проекція перпендикуляра до площини є
перпендикулярною до горизонтального сліду площини, а фронтальна – до фронтального
сліду площини.
На основі властивостей проектування прямого плоского кута можна зробити
висновок, що проекції перпендикуляра до площини будуть розміщені таким чином:
1) горизонатльна проекція ─ під прямим кутом до горизонтальної проекції горизонталі
або до горизонтального сліду площини;

22