Page 26 - 4604

Практичне заняття № 6, 7. Способи перетворення прямокутних проекцій

Мета – набути практичних навичок при розв’язуванні задач способами перетворення
прямокутних проекцій

Завдання:
1. Способом заміни площин проекцій та способом плоско-паралельного
переміщення визначити справжню величину трикутника АВС.
2. Визначити кут нахилу його до горизонтальної (варіанти 1-14) або фронтальної
(варіанти 15-28) площин проекцій.
3. Дані для свого варіанта взяти з таблиці 5.
4. Приклади виконання завдання зображено на рисунках 27, 28.

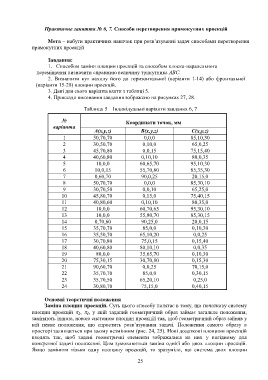
Таблиця 5 – Індивідуальні варіанти завдання 6, 7

№ Координати точок, мм
варіанта
А(x,y,z) В(x,y,z) С(x,y,z)
1 50,70,70 0,0,0 85,10,30
2 30,50,70 0,10,0 65,0,25
3 45,70,80 0,0,15 75,15,40
4 40,60,80 0,10,10 80,0,35
5 10,0,0 60,65,70 95,10,30
6 10,0,15 55,70,80 85,35,30
7 0,60,70 90,0,25 20,15,0
8 50,70,70 0,0,0 85,30,10
9 30,70,50 0,0,10 65,25,0
10 45,80,70 0,15,0 75,40,15
11 40,80,60 0,10,10 80,35,0
12 10,0,0 60,70,65 95,30,10
13 10,0,0 55,80,70 85,30,15
14 0,70,60 90,25,0 20,0,15
15 35,70,70 85,0,0 0,10,30
16 35,50,70 65,10,20 0,0,25
17 30,70,80 75,0,15 0,15,40
18 40,60,80 80,10,10 0,0,35
19 80,0,0 35,65,70 0,10,30
20 75,30,15 30,70,80 0,15,30
21 90,60,70 0,0,25 70,15,0
22 35,70,70 85,0,0 0,30,15
23 35,70,50 65,20,10 0,25,0
24 30,80,70 75,15,0 0,40,15

Основні теоретичні положення
Заміна площин проекцій. Суть цього способу полягає в тому, що початкову систему
площин проекцій  2,  1, у якій заданий геометричний образ займає загальне положення,
заміняють іншою, новою системою площин проекцій так, щоб геометричний образ зайняв у
ній певне положення, що спростить розв’язування задачі. Положення самого образу в
просторі залишається при цьому незмінним (рис. 24, 25). Нові додаткові площини проекцій
вводять так, щоб задані геометричні елементи зображалися на них у вигідному для
конкретної задачі положенні. Цим зумовлюється заміна однієї або двох площин проекцій.
Якщо замінити тільки одну площину проекцій, то зрозуміло, що система двох площин

25