Page 116 - 4560

which we will continue to study.
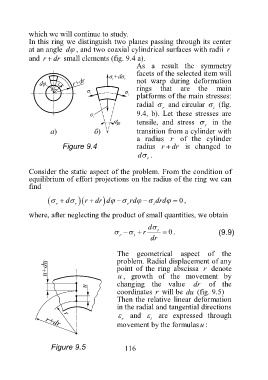
In this ring we distinguish two planes passing through its center
at an angle d , and two coaxial cylindrical surfaces with radii r
and r dr small elements (fig. 9.4 a).
As a result the symmetry
facets of the selected item will
not warp during deformation
rings that are the main
platforms of the main stresses:
radial  and circular  (fig.
r t
9.4, b). Let these stresses are
tensile, and stress  in the
r
transition from a cylinder with
a radius r of the cylinder
Figure 9.4 radius r dr is changed to
d .
r

Consider the static aspect of the problem. From the condition of
equilibrium of effort projections on the radius of the ring we can
find

  d r r dr d    r rd  t drd  0 ,
r
where, after neglecting the product of small quantities, we obtain
d
    r r  0. (9.9)
r t
dr

The geometrical aspect of the
problem. Radial displacement of any
point of the ring abscissa r denote
u , growth of the movement by
changing the value dr of the
coordinates r will be du (fig. 9.5)
Then the relative linear deformation
in the radial and tangential directions
 and  are expressed through
r t
movement by the formulasu :

Figure 9.5 116