Page 104 - 4560

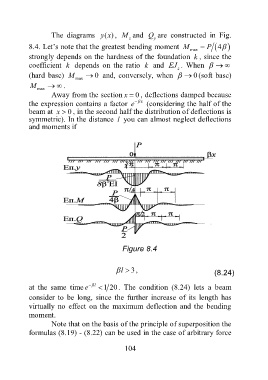
The diagrams (xy ), M and Q are constructed in Fig.
z y

8.4. Let’s note that the greatest bending moment M  P 4
max
strongly depends on the hardness of the foundation k , since the
coefficient k depends on the ratio k and EJ . When   
z
0
(hard base) M  0 and, conversely, when   (soft base)
max
M   .
max
Away from the section x  , deflections damped because
0
the expression contains a factor e   x (considering the half of the
0
beam at x  , in the second half the distribution of deflections is
symmetric). In the distance l you can almost neglect deflections
and moments if

Figure 8.4

l   3, (8.24)

at the same time e  l   1 20. The condition (8.24) lets a beam
consider to be long, since the further increase of its length has
virtually no effect on the maximum deflection and the bending
moment.
Note that on the basis of the principle of superposition the
formulas (8.19) - (8.22) can be used in the case of arbitrary force

104