Page 43 - 4498

dp dV
   0. (2.7.9)
p V

dp
So d ln  p  , then
p

ln pd   lnV  0  d ln  Vp   0 . (2.7.10)

Differential of constant magnitude is zero ,thus


p  V  const.
(2.7.11)
The derived equation (2.7.11) is called
adiabatic one or Poisson's equation (Siméon

Denis Poisson ( 1781 -1840), a French
mathematician, geometer, and physicist.) In
C
this equation special heat ratio P   is
C V

called an adiabatic index.

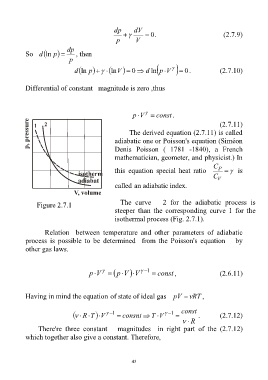
The curve 2 for the adiabatic process is
Figure 2.7.1
steeper than the corresponding curve 1 for the
isothermal process (Fig. 2.7.1).

Relation between temperature and other parameters of adiabatic
process is possible to be determined from the Poisson's equation by
other gas laws.

  1
p V  p V  V  const , (2.6.11)

Having in mind the equation of state of ideal gas pV  RT ,

 1  1 const
  R T   V  consnt  T V   . (2.7.12)
  R
There're three constant magnitudes in right part of the (2.7.12)

which together also give a constant. Therefore,

43