Page 21 - 4401

3. Вершина параболоїда перетнула дно посудини (рис.
4.6, в)

2
 gH 2  (R  R 2 )H
V   1 . (4.12)
p
 2 2

Для розв’язку диференціального рівняння (4.4)
використаємо краєві умови типу:
при r = r a, h = h a, p = p;
при r = /R 2 , h = Н п, p = p 0. (4.13)

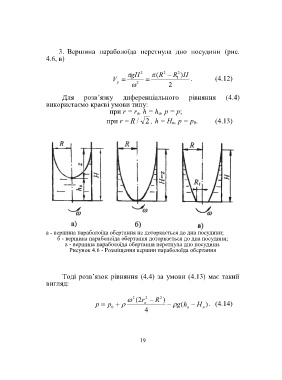
а - вершина параболоїда обертання не доторкається до дна посудини;
б - вершина параболоїда обертання доторкається до дна посудини;
в - вершина параболоїда обертання перетнула дно посудини.
Рисунок 4.6 - Розміщення вершин параболоїда обертання

Тоді розв’язок рівняння (4.4) за умови (4.13) має такий
вигляд:

2
 2 2 ( r  R 2 )
p  p   a   g (h  H ). (4.14)
0 a п
4

19