Page 24 - 4299

 
Тобто поліном P x записаний таким чином, що сума індексів при коефіцієнтах a і
N k
відповідних показників степеня – величина постійна і дорівнює N .

6
Для задачі, що розв’язується, N  і a  -2,0833;5.4688;-5,1042;3,2813;-1,1925;1.0000 ,
тобто a  1, …, a  -2,0833.
6 1
 
 
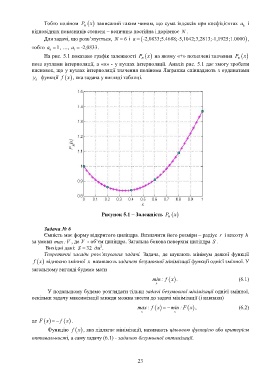
На рис. 5.1 показано графік залежності P x на якому «+» позначені значення P x
N N
поза вузлами інтерполяції, а «о» - у вузлах інтерполяції. Аналіз рис. 5.1 дає змогу зробити
висновок, що у вузлах інтерполяції значення полінома Лагранжа співпадають з ординатами
y функції   x , яка задана у вигляді таблиці.
f
k

 
Рисунок 5.1 – Залежність P x
N

Задача № 6
Ємність має форму відкритого циліндра. Визначити його розміри – радіус r і висоту h
за умови max :V , де V - об’єм циліндра. Загальна бокова поверхня циліндра S .
2
Вихідні дані: S  32 дм .
Теоретичні засади розв’язування задачі. Задача, де шукають мінімум деякої функції
f   x відносно змінної x називають задачею безумовної мінімізації функції однієї змінної. У
загальному вигляді будемо мати

min : f   x . (6.1)
x
У подальшому будемо розглядати тільки задачі безумовної мінімізації однієї змінної,
оскільки задачу максимізації завжди можна звести до задачі мінімізації (і навпаки)

max : f   x   min : F   x , (6.2)
x x
де   x   f   x .
F
f
Функцію   x , яка підлягає мінімізації, називають цільовою функцією або критерієм
оптимальності, а саму задачу (6.1) - задачею безумовної оптимізації.

23