Page 24 - 4263

Elements of Vector Algebra

this axis. ✓

−→
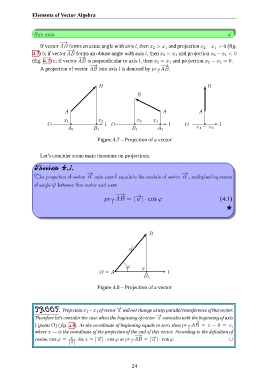
If vector AB forms an acute angle with axis l, then x 2 > x 1 and projection x 2 −x 1 > 0 (fig.
−→
4.7) b; if vector AB forms an obtuse angle with axis l, then x 2 < x 1 and projection x 2 − x 1 < 0
−→
(fig. 4.7) c; if vector AB is perpendicular to axis l, then x 2 = x 1 and projection x 2 − x 1 = 0.
−→ −→
A projection of vector AB into axis l is denoted by pr−→AB.
l

B B

B

A A A

x 1 x 2 x 2 x 1
. . . . . . . . . . . . . . . . . . . . . .
O l O l O l
x 1 = x 2
A 1 B 1 B 1 A 1
Figure 4.7 – Projection of a vector

Let’s concider some main theorems on projections.

Theorem 4.1.
The projection of vector a onto axis l equals to the module of vector a , multiplied by cosine
− →
−→
of angle φ between this vector and axis:

−→
−→
pr−→AB = | a | · cos φ (4.1)
l
⋆

B

−→
a

φ x
O = A . . . . . . . . l
B 1

Figure 4.8 – Projection of a vector

−→
PROOF. Projectionx 2 −x 1 ofvector a willnotchangeatanyparalleltransferenceofthisvector.
−→
Therefore let’s consider the case when the beginning of vector a coincides with the beginning of axis
−→
l (point O) ( fig. 4.8). As the coordinate of beginning equals to zero, then pr−→AB = x − 0 = x,
l
where x — is the coordinate of the projection of the end of this vector. According to the definition of
−→
−→
−→
cosine, cos φ = x . So, x = | a | · cos φ or pr−→AB = | a | · cos φ. 2
−→
| a | l

24